红黑树概念解析与C++实现

整理了红黑树的性质与基本操作的C++实现

基本概念

红黑树（Red Black Tree，简称R-B Tree）是一种特殊的二叉查找树([[二叉树的存储结构及其非层序遍历|二叉树]])。它的特殊性体现在：

每个节点都有颜色，可以是红色或黑色。
根节点是黑色。
每个叶子节点（NULL）是黑色。尤其注意这里的结子节点指的是NULL。
红色节点的子节点必为黑色。
任一结点到其所有后代叶节点的路径中具有相同数目的黑色节点。

特性5保证了任一路径不会超过最短路径的两倍，因而红黑树是接近平衡的二叉树。

存储结构

一个红黑树节点可以使用三叉链表的形式实现为：

struct R_BNode {
    enum COLOR {BLACK = 0, RED = 1};

    explicit R_BNode(int data = 0, R_BNode::COLOR color = RED) 
        : left_(Nil), right_(Nil), parent_(Nil)
        , color_(color), data_(data)  {}

    R_BNode *left_;
    R_BNode *right_;
    R_BNode *parent_;
    COLOR color_;
    int data_;

    static R_BNode *Nil;
};

R_BNode *R_BNode::Nil = new R_BNode(0, R_BNode::BLACK);

这里为简化问题将data定为int类型，这并不会影响对红黑树的研究。如有需要可以使用类模板或void*等方式来实现泛型的红黑树。

定义红黑树类型为指向红黑树节点的指针。并创建一个静态变量Nil作为所有叶子节点的指代，这样做就可以把本不存在的叶子节点视为普通节点来处理了。

红黑树可以实现如下：

struct R_BTree {
    explicit R_BTree() : root_(R_BNODE::Nil) {}
    
    R_BNode *root_;
};

基本操作：旋转

概念

当修改红黑树上的节点时，可能会破坏树的性质，使得树不再是红黑树。此时需要调整一些节点的颜色与指针结构，使树重新成为红黑树。

其中对指针结构的调整就需要借助旋转操作，这是一种能保持二叉搜索树性质的局部操作。旋转分为左旋与右旋，下面以左旋为例介绍旋转操作：

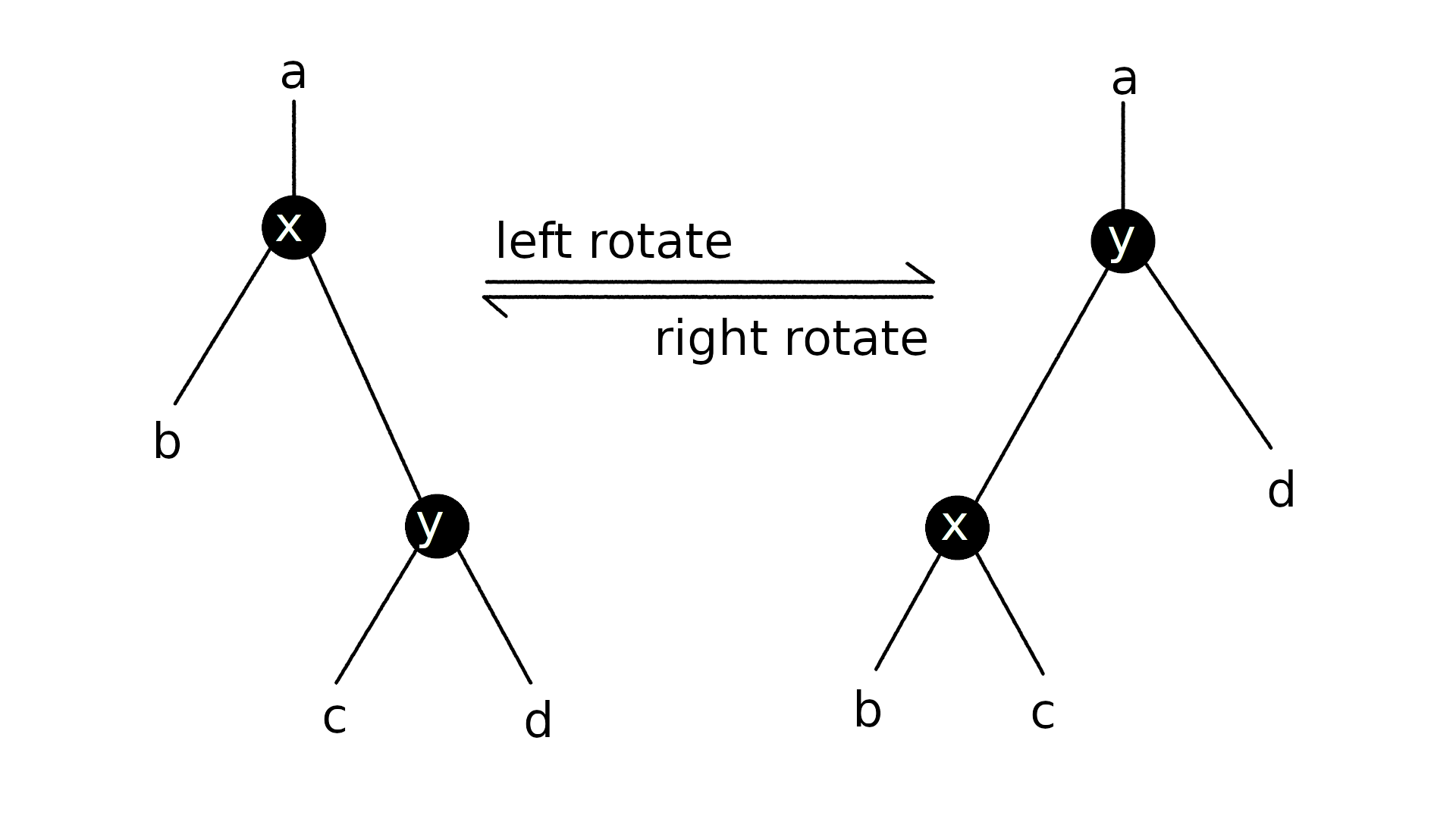
任一右孩子不为Nil的结点x都可进行左旋操作，设其右孩子是y，则左旋后：

y成为子树新的根节点。
x在新子树中成为y的左孩子。
上述变化后，x的右孩子变成双亲了，空出一个位置，而y原来的左孩子无家可归，由此让y原来的左孩子成为x新的右孩子。

而右旋是左旋的镜像操作。两种旋转如下图所示：

实现

// 仅给出实现，声明可以自行添加到对应的类中
void R_BTree::LeftRotate(R_BNode *x) {
    if (x->right_ == R_BNode::Nil) throw "Error while left rotate";

    auto y = x->right_;
    x->right_ = y->left_;
    if (y->left_ != R_BNode::Nil) {
        y->left_->parent_ = x;
    }

    y->parent_ = x->parent_;
    if (x->parent_ == R_BNode::Nil) {
        root_ = y;
    } else if (x == x->parent_->left_) {
        x->parent_->left_ = y;
    } else {
        x->parent_->right_ = y;
    }

    y->left_ = x;
    x->parent_ = y;
}

void R_BTree::RightRotate(R_BNode *x) {
    if (x->left_ == R_BNode::Nil) throw "Error while right rotate";

    auto y = x->left_;
    x->left_ = y->right_;
    if (y->right_ != R_BNode::Nil) {
        y->right_->parent_ = x;
    }

    y->parent_ = x->parent_;
    if (x->parent_ == R_BNode::Nil) {
        root_ = y;
    } else if (x == x->parent_->left_) {
        x->parent_->left_ = y;
    } else {
        x->parent_->right_ = y;
    }

    y->right_ = x;
    x->parent_ = y;
}

基本操作：插入

红黑树是一种特殊的二叉查找树，因此插入节点时先按照二叉查找树的方法进行插入：

void R_BTree::Insert(int value) {
    auto y = R_BNode::Nil;
    auto x = root_;
    auto z = new R_BNode(value, R_BNode::RED);
    while (x != R_BNode::Nil) {
        y = x;
        if (value < x->data_) {
            x = x->left_;
        } else {
            x = x->right_;
        }
    }
    z->parent_ = y;
    if (y = R_BNode::Nil) {
        root_ = z;
    } else if (z->data_ < y->data_) {
        y->left_ = z;
    } else {
        y->right_ = z;
    }
    InsertFixup(z);
}

这样一来我们可能破坏了树的结构，因此，我们寄希望于最后调用的InsertFixup函数。

如何实现InsertFixup函数呢？这就得慢慢分析：

规则1：节点有颜色，且是红色或黑色。

规则3：叶子节点是黑色节点。

这两条显然是不会违反的。

规则5：任一结点到其所有后代叶节点的路径中具有相同数目的黑色节点。

这就是我们插入的节点总是红色的原因，插入红色的结点并不影响树中原有路径中的黑色节点数目。因此不会违反规则5。

规则2：根节点是黑色节点。

当我们插入的节点作为根节点时，就违反了规则2。此时只要改变节点的颜色就可以修复红黑树。此时可以实现出：

void R_BTree::InsertFixup(R_BNode *z) {
    ...
    root_->color = R_BNode::BLACK;
}

规则4：红色节点的孩子一定是黑色节点。

当插入节点的父节点是红色时，违反规则4。总共存在三种可能的情况：

情况一：叔节点是红色

此时将叔节点与父节点都设为黑色，并把祖父节点设为红色。然后对祖父节点使用InsertFixup函数即可。因为对祖父节点的任何子孙节点，都必然途径祖父节点，以及父节点、叔节点中的一个。将父节点与叔节点都设成黑色等于所有路径的黑色节点数加一，而将祖父节点设为红色等于所有路径的黑色节点数减一。因此不会违反规则5。同时这样将规则4的违反提升到了更高的层次去处理，这样至多处理log(h)（h为树高）次。

void R_BTree::InsertFixup(R_BNode *z) {
    while (z->parent->color == R_BNode::RED) {
        if (z->parent_ = z->parent_->parent_->left_) {
            auto y = z->parent_->parent_->right_;
            // case 1
            if (y->color_ = R_BNode::RED) {
                z->parent_->color_ == R_BNode::BLACK;
                y->color_ = R_BNode::BLACK;
                z->parent_->parent_->color_ = R_BNode::RED;
                z = z->parent_->parent_;
                continue;
            }
            ...
        } else {
            auto y = z->parent_->parent_->left_;
            // case 1
            if (y->color_ = R_BNode::RED) {
                z->parent_->color_ == R_BNode::BLACK;
                y->color_ = R_BNode::BLACK;
                z->parent_->parent_->color_ = R_BNode::RED;
                z = z->parent_->parent_;
                continue;
            } 
            ...
        }
    }
    root_->color = R_BNode::BLACK;
}

情况二：叔节点是黑色，且z与父节点异侧

所谓同侧，就是说z相对于父节点的方向和父节点相对于祖父节点的方向相同。如都是左孩子或都是右孩子。异侧则反之。

此时可以通过对父节点的一次旋转将情况二转化为情况三。

情况三：叔节点是黑色，且z与父节点同侧

此时对祖父节点进行一次与情况二反向的旋转即可修复红黑树。

以一个不同侧且父节点为左孩子的情况为例：

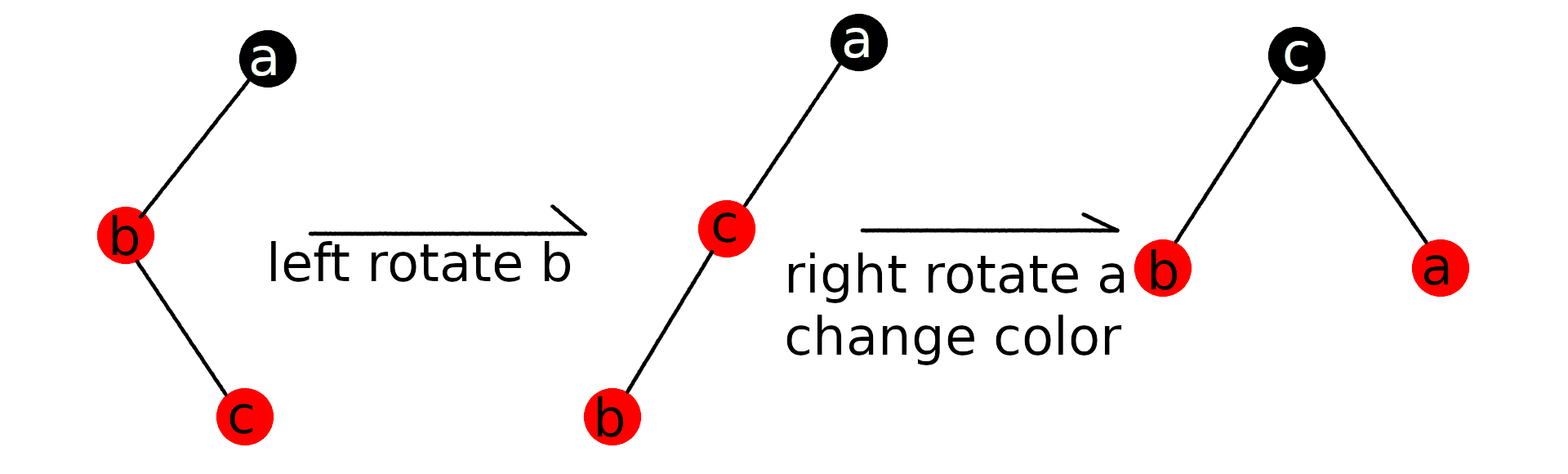
如上图，对c而言，叔节点是Nil，为黑色。且c是b的右孩子，而b是a的左孩子，因此c与父节点不同侧，即为情况2。

此时要想使bc同侧，只需对b进行左旋，并将b当做插入节点重新考虑。显然一次左旋过后，b的叔节点为Nil，为黑色。且与父节点c同侧。即为情况3。

此时只需交换父节点与祖父节点的颜色，并对祖父节点进行右旋，即可完成对红黑树的修复。

注意：上述旋转方向是父节点为左孩子时的情况，对于父节点为右孩子的情况，需要进行镜像操作，即左右互换。

最终实现为：

void R_BTree::InsertFixup(R_BNode *z) {
    while (z->parent_->color_ == R_BNode::RED) {
        if (z->parent_ == z->parent_->parent_->left_) {
            auto y = z->parent_->parent_->right_;
            // case 1
            if (y->color_ == R_BNode::RED) {
                z->parent_->color_ = R_BNode::BLACK;
                y->color_ = R_BNode::BLACK;
                z->parent_->parent_->color_ = R_BNode::RED;
                z = z->parent_->parent_;
                continue;
            } else if (z == z->parent_->right_) {
                //case 2
                z = z->parent_;
                LeftRotate(z);
            }
            // case 3
            z->parent_->color_ = R_BNode::BLACK;
            z->parent_->parent_->color_ = R_BNode::RED;
            RightRotate(z->parent_->parent_);
        } else {
            auto y = z->parent_->parent_->left_;
            // case 1
            if (y->color_ == R_BNode::RED) {
                z->parent_->color_ = R_BNode::BLACK;
                y->color_ = R_BNode::BLACK;
                z->parent_->parent_->color_ = R_BNode::RED;
                z = z->parent_->parent_;
                continue;
            } else if (z == z->parent_->left_) {
                //case 2
                z = z->parent_;
                RightRotate(z);
            }
            // case 3
            z->parent_->color_ = R_BNode::BLACK;
            z->parent_->parent_->color_ = R_BNode::RED;
            LeftRotate(z->parent_->parent_);
        }
    }
    root_->color_ = R_BNode::BLACK;
}

基本操作：删除

要删除一个节点，首先要定义一个辅助操作，用以使用一个节点去替换另一个节点的位置。

// 使用v去替换u
void R_BTree::Transplant(R_BNode *u, R_BNode *v) {
    if (u->parent_ == R_BNode::Nil) {
        root_ = v;
    } else if (u == u->parent_->left_) {
        u->parent_->left_ = v;
    } else {
        u->parent_->right_ = v;
    }
    v->parent_ = u->parent_;
}

删除一个节点的操作与二叉搜索树相似，当目标节点只有两个以下孩子时，使用它的孩子替换它自身。当目标节点存在两个孩子时则比较麻烦，需要找出目标节点的后继，并使用这个后继替换自身。

void R_BTree::Delete(R_BNode *z) {
    auto y = z;
    auto y_origin_color = z->color_;
    R_BNode *x = nullptr;
    if (z->left_ == R_BNode::Nil) {
        x = z->right_;
        Transplant(z, z->right_);
    } else if (z->right_ == R_BNode::Nil) {
        x = z->left_;
        Transplant(z, z->left_);
    } else {
        y = z->right_;
        while (y->left_ != R_BNode::Nil) {
            y = y->left_;
        }
        y_origin_color = y->color_;
        x = y->right_;
        if (y->parent_ != z) {
            Transplant(y, y->right_);
            y->right_ = z->right_;
            y->right_->parent_ = y;
        } 
        Transplant(z, y);
        y->left_ = z->left_;
        y->left_->parent_ = y;
        y->color_ = z->color_;
    }
    if (y_origin_color == R_BNode::BLACK) {
        DeleteFixup(x);
    }
}

这段程序中，y用来标记删除或移动的节点。x用来标记y在移动或删除之前的位置。如果y是红色节点，那么移动或删除y并不会破坏红黑树的性质。因为：

树的黑高（只计算黑色节点时的高度）没有改变。
y移动到z的位置并继承了z的颜色，而z的位置与颜色在删除操作前是合法的，因此y不会改变该位置合法性。
如果y为红色，则y不是根结点，因此根结点仍为黑色。

现在考虑对破坏的修复，如果y黑色，将导致3个问题：

如果y是原来的节结点，而继承它位置的节点是红色，则违反了性质2。
如果x和x.p是红色的，则违反了性质4。
移动y导致先前树中所有包含y的简单路径中黑色节点的数目减一，导致了所有y的祖先节点都不符合性质5。

解决办法是将占有了y原来位置的节点x视为还有一层额外的黑色，这使得性质5成立，但因为现在的x要么是红黑色（颜色属性为红）要么是双重黑色（颜色属性为黑），又违反了性质1。注意这里所说的额外黑色是针对x节点的，并不反应在节点的颜色属性上。

对于x，如果：

x是红黑色，则可以将x着为黑色。
x是根结点，则可以简单的消去一层黑色，什么也不做。

void R_BTree::DeleteFixup(R_BNode *x) {
    if(x == root_ || x->color_ == R_BNode::RED) {
        x->color_ = R_BNode::BLACK;
        return;
    }
}

此时要修复红黑树，需要分成4种情况：

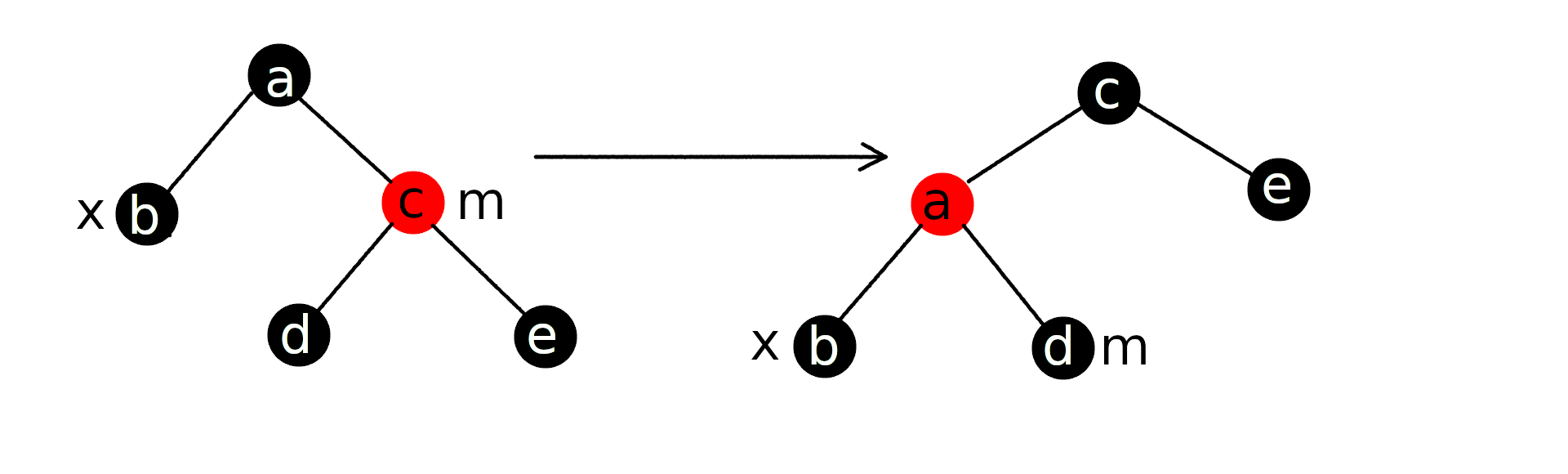
情况1：x的兄弟节点m为红色

此时由于m的两个子节点都为黑色，可以改变m和父节点的颜色，然后对父节点进行一次旋转。并令x的新兄弟节点为新的m，这样情况就转移到了2、3或4。

此时可以实现为：

void R_BTree::DeleteFixup(R_BNode *x) {
    if(x == root_ || x->color_ == R_BNode::RED) {
        x->color_ = R_BNode::BLACK;
        return;
    }
    if (x == x->parent_->left_) {
        auto m = x->parent_->right_;
        // case 1
        if (m->color_ == R_BNode::RED) {
            m->color_ = R_BNode::BLACK;
            x->parent_->color_ = R_BNode::RED;
            LeftRotate(x->parent_);
            m = x-parent_->right_;
        }
        ...
    } else {
        auto m = x->parent_->left_;
        // case 1
        if (m->color_ == R_BNode::RED) {
            m->color_ = R_BNode::BLACK;
            x->parent_->color_ = R_BNode::RED;
            RightRotate(x->parent_);
            m = x-parent_->left_;
        }
        ...
    }
}

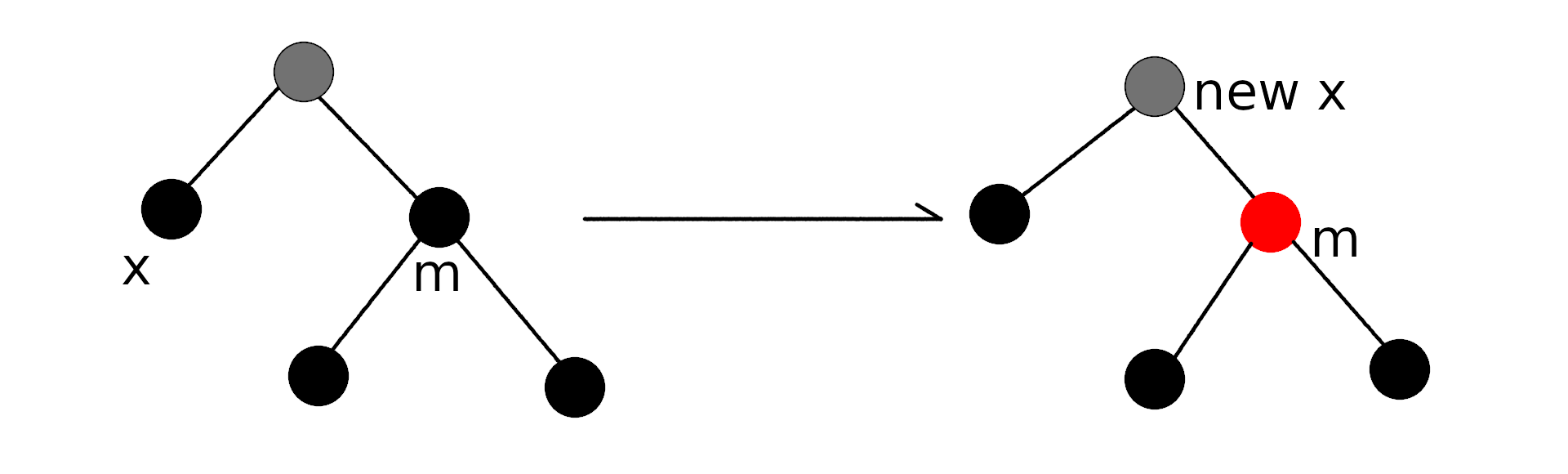
情况2：x的兄弟节点m为黑色，且m的两个子节点都为黑色

此时由于x是双重黑色，而m与其两个子节点构成了两层黑色，因此可以从x与m上分别消去一层黑色，使得x为黑色，而m为红色。并令x->parent_为新的x，并对其进行DeleteFixup。

此时由于重复调用，改变之前的程序结构：

void R_BTree::DeleteFixup(R_BNode *x) {
    while(x != root_ && x->color_ != R_BNode::RED) {
       if (x == x->parent_->left_) {
           auto m = x->parent_->right_;
           // case 1
           if (m->color_ == R_BNode::RED) {
               m->color_ = R_BNode::BLACK;
               x->parent_->color_ = R_BNode::RED;
               LeftRotate(x->parent_);
               m = x-parent_->right_;
           }
           // case 2
           if (m->left_->color_ == R_BNode::BLACK
               && m->right_->color_ == R_BNode::BLACK) {
               m->color_ = R_BNode::RED;
               x = x->parent_;
               continue;
           }
           ...
        } else {
           auto m = x->parent_->left_;
           // case 1
           if (m->color_ == R_BNode::RED) {
               m->color_ = R_BNode::BLACK;
               x->parent_->color_ = R_BNode::RED;
               RightRotate(x->parent_);
               m = x-parent_->left_;
           }
           // case 2
           if (m->left_->color_ == R_BNode::BLACK
               && m->right_->color_ == R_BNode::BLACK) {
               m->color_ = R_BNode::RED;
               x = x->parent_;
               continue;
           }
           ...
        }
    }
     x->color_ = R_BNode::Black;
}

情况3：x的兄弟节点m为黑色，且m的异侧孩子为红色，同侧孩子为黑色

此时交换m与异侧孩子的颜色，并进行旋转。使m的异侧孩子成为x新的兄弟节点，m成为新m的同侧孩子。这样就转化成了情况4。

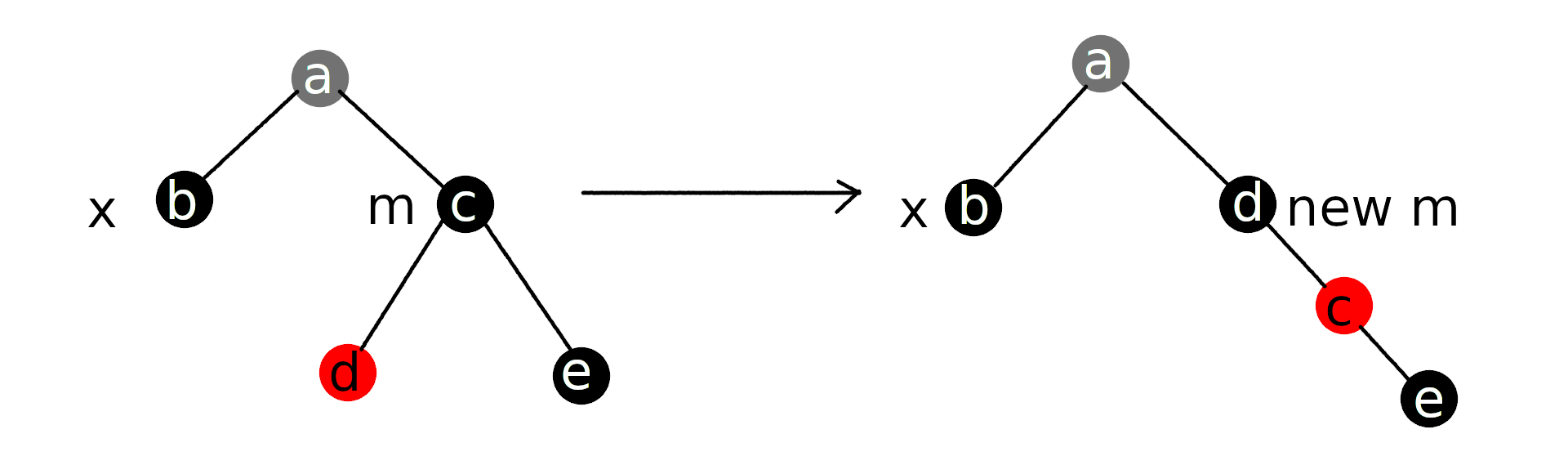
实现为：

void R_BTree::DeleteFixup(R_BNode *x) {
    while(x != root_ && x->color_ != R_BNode::RED) {
       if (x == x->parent_->left_) {
           auto m = x->parent_->right_;
           // case 1
           if (m->color_ == R_BNode::RED) {
               m->color_ = R_BNode::BLACK;
               x->parent_->color_ = R_BNode::RED;
               LeftRotate(x->parent_);
               m = x-parent_->right_;
           }
           // case 2
           if (m->left_->color_ == R_BNode::BLACK
               && m->right_->color_ == R_BNode::BLACK) {
               m->color_ = R_BNode::RED;
               x = x->parent_;
               continue;
           } else if (m->left_->color_ == R_BNode::RED
                     && m->right_color_ == R_BNode::BLACK) {
               // case 3
               m->color_ = R_BNode::RED;
               m->left_->color_ = R_BNode::BLACK;
               RightRotate(m);
               m = x->parent_->right_;
           }
           
           ...
        } else {
           auto m = x->parent_->left_;
           // case 1
           if (m->color_ == R_BNode::RED) {
               m->color_ = R_BNode::BLACK;
               x->parent_->color_ = R_BNode::RED;
               RightRotate(x->parent_);
               m = x-parent_->left_;
           }
           // case 2
           if (m->left_->color_ == R_BNode::BLACK
               && m->right_->color_ == R_BNode::BLACK) {
               m->color_ = R_BNode::RED;
               x = x->parent_;
               continue;
           } else if (m->right_->color_ == R_BNode::RED
                     && m->left_color_ == R_BNode::BLACK) {
               // case 3
               m->color_ = R_BNode::RED;
               m->right_->color_ = R_BNode::BLACK;
               LeftRotate(m);
               m = x->parent_->left_;
           }
           ...
        }
    }
     x->color_ = R_BNode::BLACK;
}

情况4：x的兄弟节点为黑色，且m的同侧孩子为红色。

使m为父节点的颜色，并将父节点与m的同侧孩子设为黑色。对父节点进行旋转，使m成为新的取代父节点的位置，并设x为根节点。即可修复红黑树。

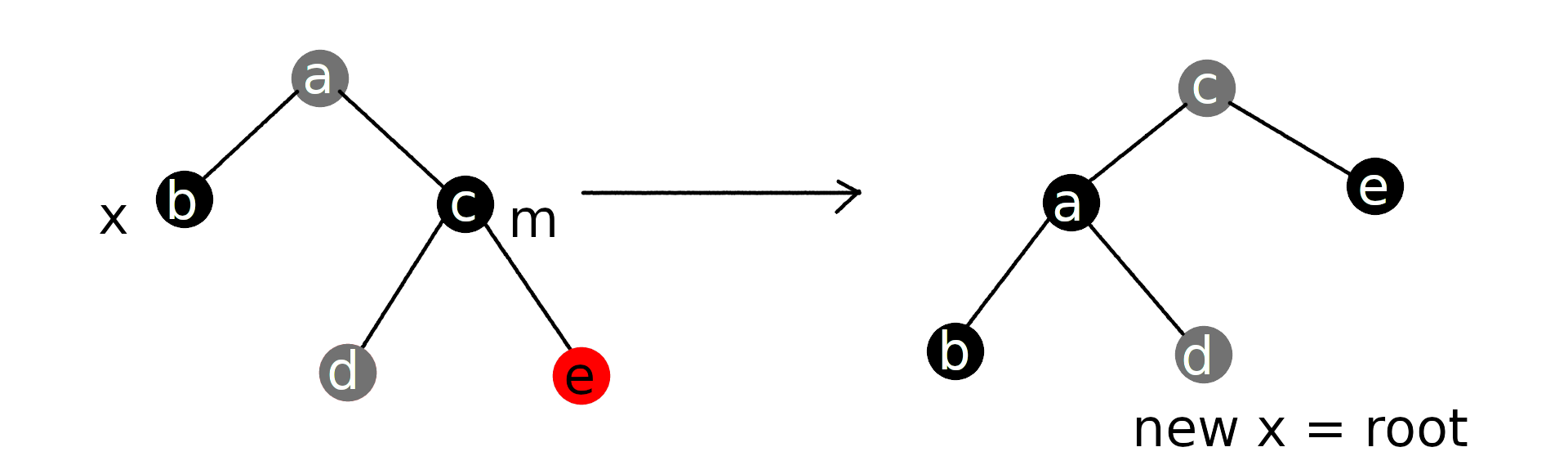
此时得出了最终实现：

void R_BTree::DeleteFixup(R_BNode *x) {
    while(x != root_ && x->color_ != R_BNode::RED) {
       if (x == x->parent_->left_) {
           auto m = x->parent_->right_;
           // case 1
           if (m->color_ == R_BNode::RED) {
               m->color_ = R_BNode::BLACK;
               x->parent_->color_ = R_BNode::RED;
               LeftRotate(x->parent_);
               m = x->parent_->right_;
           }
           // case 2
           if (m->left_->color_ == R_BNode::BLACK
               && m->right_->color_ == R_BNode::BLACK) {
               m->color_ = R_BNode::RED;
               x = x->parent_;
               continue;
           } else if (m->left_->color_ == R_BNode::RED
                     && m->right_->color_ == R_BNode::BLACK) {
               // case 3
               m->color_ = R_BNode::RED;
               m->left_->color_ = R_BNode::BLACK;
               RightRotate(m);
               m = x->parent_->right_;
           }
           // case 4
           m->color_ = x->parent_->color_;
           x->parent_->color_ = R_BNode::BLACK;
           m->right_->color_ = R_BNode::BLACK;
           LeftRotate(x->parent_);
           x = root_;
        } else {
           auto m = x->parent_->left_;
           // case 1
           if (m->color_ == R_BNode::RED) {
               m->color_ = R_BNode::BLACK;
               x->parent_->color_ = R_BNode::RED;
               RightRotate(x->parent_);
               m = x->parent_->left_;
           }
           // case 2
           if (m->left_->color_ == R_BNode::BLACK
               && m->right_->color_ == R_BNode::BLACK) {
               m->color_ = R_BNode::RED;
               x = x->parent_;
               continue;
           } else if (m->right_->color_ == R_BNode::RED
                     && m->left_->color_ == R_BNode::BLACK) {
               // case 3
               m->color_ = R_BNode::RED;
               m->right_->color_ = R_BNode::BLACK;
               LeftRotate(m);
               m = x->parent_->left_;
           }
           // case 4
           m->color_ = x->parent_->color_;
           x->parent_->color_ = R_BNode::BLACK;
           m->left_->color_ = R_BNode::BLACK;
           LeftRotate(x->parent_);
           x = root_;
        }
    }
     x->color_ = R_BNode::BLACK;
}

总结

红黑树是一种特殊的二叉搜索树，因此适用二叉搜索树的所有不改变树结构的操作。而对于改变了红黑树结构的操作则需要牢记，主要分为旋转、插入和删除。