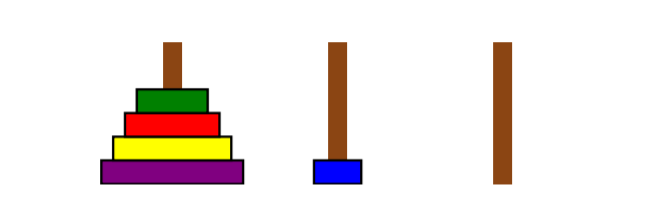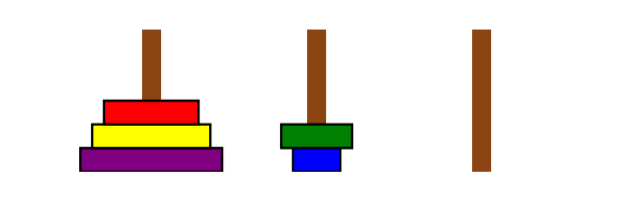Haskell解决四柱汉诺塔问题

回顾：汉诺塔是什么？

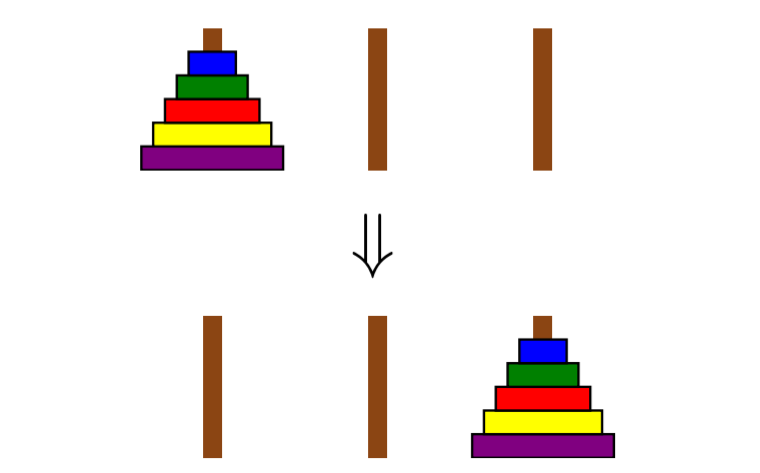
The Towers of Hanoi is a classic puzzle with a solution that can be described recursively. Disks of different sizes are stacked on three pegs; the goal is to get from a starting configuration with all disks stacked on the first peg to an ending configuration with all disks stacked on the last peg, as shown in Figure 1.

​ Figure 1: The Towers of Hanoi The only rules are • you may only move one disk at a time, and • a larger disk may never be stacked on top of a smaller one. For example, as the first move all you can do is move the topmost, smallest disk onto a different peg, since only one disk may be moved at a time.

​ Figure 2: A valid first move. From this point, it is illegal to move to the configuration shown in Figure 3, because you are not allowed to put the green disk on top of the smaller blue one.

​ Figure 3: An illegal configuration. To move n discs (stacked in increasing size) from peg a to peg b using peg c as temporary storage,

1. move n − 1 discs from a to c using b as temporary storage
2. move the top disc from a to b
3. move n − 1 discs from c to b using a as temporary storage.

这东西相信大家都非常熟悉了，不多缀言。下面进入第一个问题，使用Haskell求解汉诺塔。

Haskell求解汉诺塔

Given the number of discs and names for the three pegs, hanoi should return a list of moves to be performed to move the stack of discs from the first peg to the second.

先上代码：

type Peg = String
type Move = (Peg, Peg)
-- hanoi numOfDiscs->originPeg->targetPeg->otherPeg->moves
hanoi :: Integer->Peg->Peg->Peg->[Move]
hanoi 0 a b c = []
hanoi n a b c = hanoi (n - 1) a c b ++ [(a, b)] ++ hanoi (n - 1) c b a

这几行程序没费什么力，使我深深地体会到了Haskell的简洁与优雅，这种写法实在是太漂亮了。这里用了很简单的一个思路，hanoi n a b c表示由a柱，经c柱移动n个盘子到b柱。

hanoi n a b c = hanoi (n - 1) a c b ++ [(a, b)] ++ hanoi (n - 1) c b a

这句代码表达先把上层 n - 1个盘子由a柱移动到c柱，再把最底层盘子直接移动到b柱，最后把c柱上的盘子也移动到b柱。Haskell这种写法在简洁与表达力上实在是令我惊叹。

再来一根：四柱汉诺塔问题

顾名思义，四柱汉诺塔就是在三柱汉诺塔的基础上再加一根柱子。同样是求将一根柱子上的盘子全部移动到另一根上的过程序列。

解四柱汉诺塔的基本思路是由a柱，经过b柱、d柱的辅助，将一部分盘子移动到c柱。

由于所有先移出去的盘子一定比剩下任一的盘子小，在移动剩下的盘子时就无法再借助c柱了，问题变成两个三柱汉诺塔问题：

1. 由a柱经过b柱的辅助将除最下层盘子外的盘子移动到d柱；
2. 将最下层盘子移动到b柱；
3. 由d柱经过a柱的辅助将盘子移动到b柱

现在的状态是，a柱、d柱上没有盘子，c柱上有一开始移动出去的盘子，b柱上有剩下的盘子。由于c柱上的盘子都小于b柱上的盘子，故而在移动时可以借助b柱。则由c柱经过a柱、d柱的辅助将盘子移动到b柱上，即完成了将所有盘子由a柱移动到b柱的过程。

那么应该怎么把盘子分成两份呢？这里简单起见，将盘子平分成两分。

hanoiPlus :: Integer->Peg->Peg->Peg->Peg->[Move]
hanoiPlus 0 _ _ _ _ = []
hanoiPlus n a b c d = hanoiPlus (left - k) a c b d
            ++ hanoi k a d b
            ++ [(a, b)]
            ++ hanoi k d b a
            ++ hanoiPlus (left - k) c b a d
    where   
        left = n - 1
        k = n `div` 2

你的时间非常值钱：四柱汉诺塔最优解

平分是无法达到最优效率的，因为3柱移动比4柱移动耗时，要达到最优效率，需要加一个分割函数。

hanoiPlus :: Integer->Peg->Peg->Peg->Peg->[Move]
hanoiPlus 0 _ _ _ _ = []
hanoiPlus n a b c d = hanoiPlus (left - k) a c b d
            ++ hanoi k a d b
            ++ [(a, b)]
            ++ hanoi k d b a
            ++ hanoiPlus (left - k) c b a d
    where   
        left = n - 1
        k = minimalDivide n

minimalDivide :: Integer->Integer
minimalDivide 0 = 0
minimalDivide n = head (minimalDivideList n)

minimalDivideList :: Integer->[Integer]
minimalDivideList 0 = []
minimalDivideList n = minimalDivideList' [1,2..n] []
    where
        minimalDivideList' :: [Integer]->[Integer]->[Integer]
        minimalDivideList' (x:xs) [] = minimalDivideList' xs (0:[])
        minimalDivideList' [] ys = ys
        minimalDivideList' (x:xs) (y:ys) = minimalDivideList' xs ((cur):(y:ys))
            where
                cur = if x - y <= 1 || (hanoiPlus' x y) <= (hanoiPlus' x (y + 1))
                    then y else y + 1
                hanoiPlus' :: Integer->Integer->Integer
                hanoiPlus' 0 _ = 0
                hanoiPlus' n' divide = 
                    2 * (hanoiPlus' left' divide')
                    + (2^divide - 1) * 2 + 1
                    where 
                        left' = n' - divide - 1
                        divide' = if left' == 0 then 0 
                            else (reverse (y:ys))!!fromInteger(left' - 1)