字符串匹配算法半壁江山之KMP算法。
KMP算法介绍
KMP算法是一种利用模式串中的信息来尽可能减少与待匹配串的匹配次数从而大副提高效率的算法。它的核心是一个next表,用以记录一次匹配失败后,下次匹配开始的位置。
KMP匹配过程
如何生成next表是KMP的核心内容,但在此之前,不妨先看看KMP算法是如何工作的。
设模式串为”ABAABAC”,待匹配串为”ABABAABAABAC”。根据模式串生成的next表为:{0,
0, 1, 1, 2, 3,
0}。之后会介绍如何生成next表。这里先解释这个表的意义,next[n] = k意为在模式串前n位构成的子串中,其最长相等严格前后缀的长度为k。
解释一下黑体字就是说,对于模式串“ABAABAC”而言,其前6位构成的子串是”ABAABA”。所谓的严格前/后缀就是指除了串本身的前/后缀:{前/后缀} - {串本身}。相等严格前后缀是指既是串的严格前缀也是串的严格后缀的子串,对于”ABAABA”而言,其相等严格前后缀有:“A”、“ABA”两个。最长相等严格前后缀显然就是”ABA”。
上面这段话就可以表示为next[6] = 3。
从位置0开始匹配,结果如下:
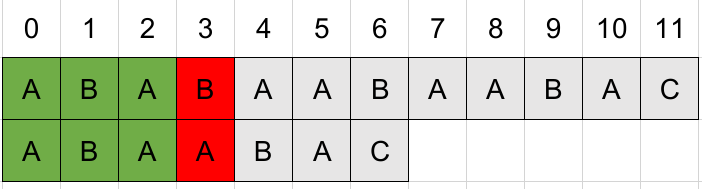
成功匹配的位数是3,查询匹配表项next[3] = 1。也就是已匹配部分的末位与首位相等,因此可以直接将首位移到末位位置开始下一轮匹配:
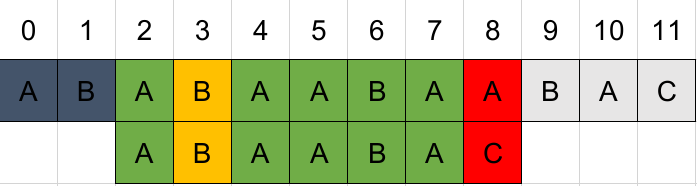
成功匹配的位数是6,注意匹配并不是从位置2开始的,而是从位置3——上次匹配失败的位置开始,查询匹配表项next[6] = 3。说明已匹配部分前3位与后3位相等,将前3位移到后3位的位置开始下一轮匹配:
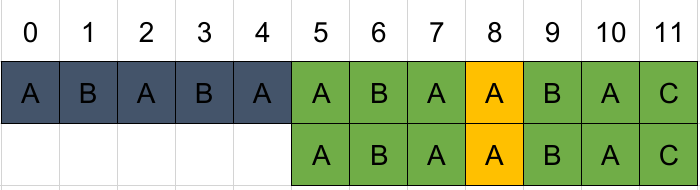
匹配成功。
注意到,所谓移动其实就是从模式串的下标next[匹配成功位数]开始,从失败位置继续匹配。
代码表示:
// str:待匹配串, pattern:模式串, next[pattern.size()]:失配表
vector<int> kmp(const string& str, const string& pattern) {
vector<int> result;
int j = 0;
for (int i = 0; i < str.size(); ++i) {
// j与i匹配失败而j不为0时,说明有j - 1位匹配成功。
// 尝试使用pattern[next[j - 1]]从失败位置继续匹配,直到
// 1. j == 0
// 2. 匹配成功
while (j > 0 && pattern[j] != str[i]) {
j = next[j - 1];
}
// 匹配成功则成功位数+1
if (pattern[j] == str[i]) {
++j;
}
// 若匹配成功位数等于模式串大小,说明模式匹配成功,记录下这个位置。
if (j == pattern.size()) {
result.push_back(i - pattern.size() + 1);
j = next[j - 1];
}
}
return result;
}next表生成
next表的生成方法可以理解成使用模式串去匹配自身。数学证明太过复杂按下不表,先上代码:
vector<int> next(const string &str) {
vector<int> result(str.length(), 0);
int k = 0;
for (int i = 1; i < result.size(); ++i) {
// k > 0且匹配失败说明之前存在k - 1位的匹配成功。
// 尝试使用str[result[k - 1]]与str[i]继续匹配
while (k > 0 && str[k] != str[i]) {
k = result[k - 1];
}
// 如果匹配成功,则说明str前i位这个子串的后k位与前k位相同
// 即result[i] = k;
if (str[k] == str[i]) {
++k;
}
result[i] = k;
}
return result;
}可以看出与kmp匹配过程的代码非常相似,图解如下:
例P=“ABCDABA”
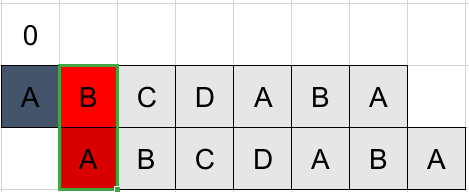
因为严格前/后缀不能等于自身,因此从第2位开始匹配,并将第一位结果置0。可见匹配失败,且k=0,将此位结果置0,进入下一位。
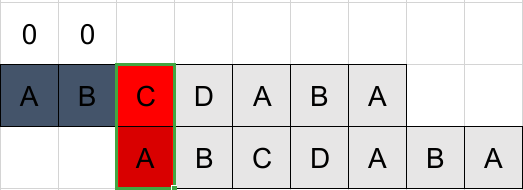
依然不匹配,且k=0,置0进入下一位。
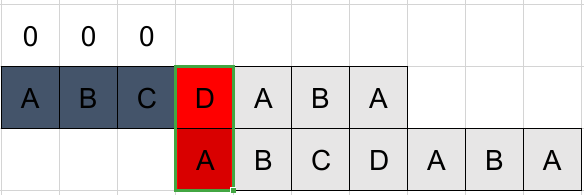
还是不匹配,且k=0,置0进入下一位。
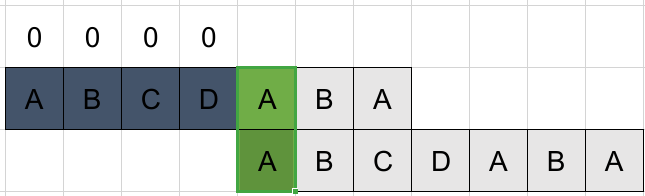
匹配,++k,并置结果=k=1。由于下一步比较时k=1增量与比较步长相同,看起来好像没有移动。
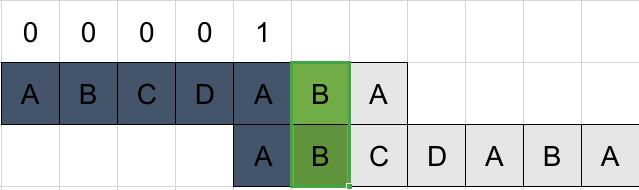
匹配,++k,并置结果=k=2。进入下一步。
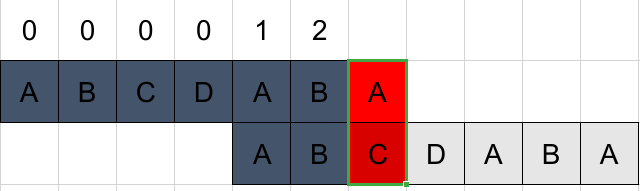
不匹配,且k > 0试图取next[k - 1] = next[1] = 0与该位比较。
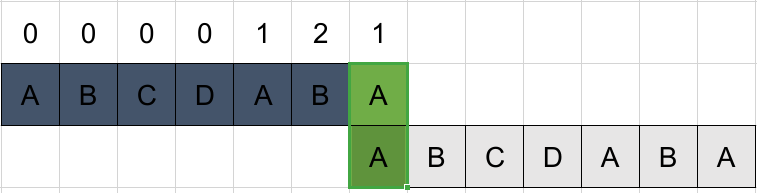
匹配,且k=0,++k置结果=k=1。结束匹配过程。
最终结果next={0,0,0,0,1,2,1}。